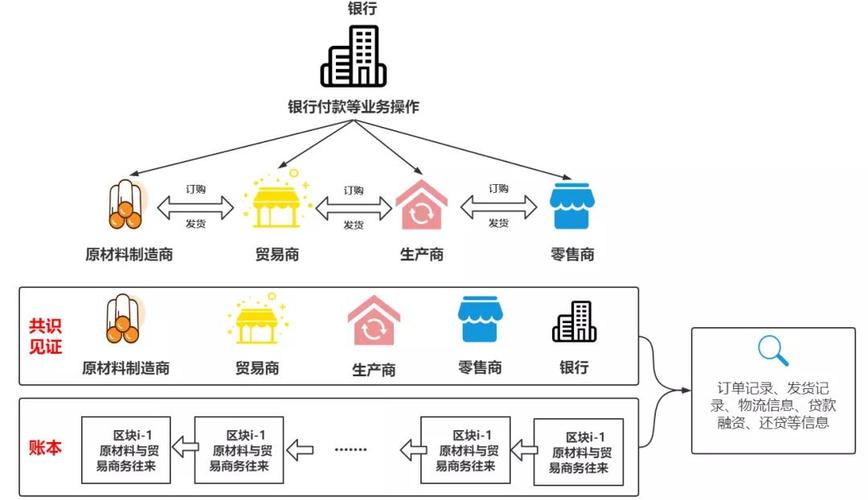
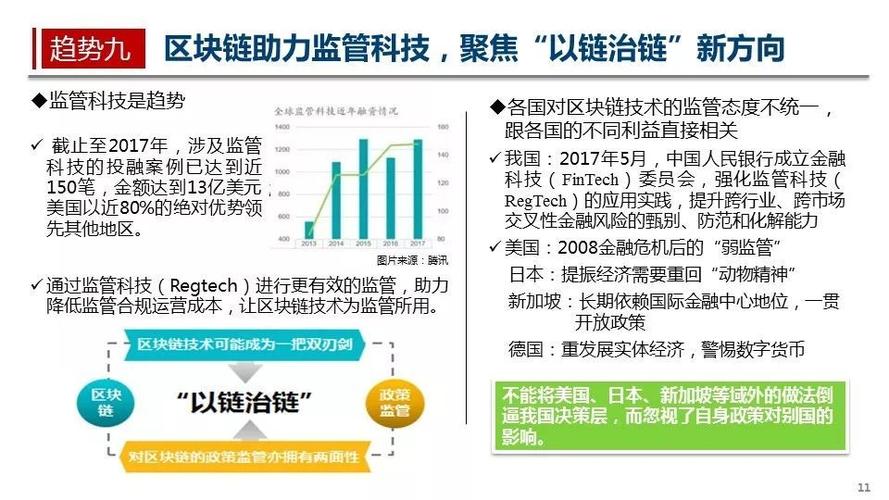
三角函数图像区间公式
区块链中的三角函数图像
在区块链领域,三角函数图像通常与密码学和加密技术相关联。这些函数在区块链中的应用包括密钥生成、哈希函数和椭圆曲线加密等方面。让我们深入了解这些关系。
在区块链中,参与者需要密钥对来进行身份验证和加密通信。常用的密钥生成算法之一是基于椭圆曲线的算法,例如椭圆曲线数字签名算法(ECDSA)。
椭圆曲线是一类特殊的曲线,其方程形式为:
\[y^2 = x^3 ax b\]其中 \(a\) 和 \(b\) 是曲线的参数。这些曲线具有一些有趣的性质,其中之一是在有限域上的运算。对于有限域 \(F_p\),我们可以定义加法和乘法操作,使得椭圆曲线上的点满足加法运算。通过选择合适的参数 \(a\)、\(b\) 和素数 \(p\),可以得到适合密码学用途的椭圆曲线。
密钥生成过程涉及选择一个随机数 \(k\),然后计算椭圆曲线上的点 \(kG\),其中 \(G\) 是曲线上的一个固定点(称为生成点)。公钥即为 \(kG\),私钥为 \(k\)。
在区块链中,哈希函数是至关重要的。哈希函数将任意长度的输入数据映射为固定长度的输出,通常用于数据完整性验证和密码学安全。
常用的哈希函数包括 SHA-256(Secure Hash Algorithm 256-bit),它将输入数据映射为一个 256 位的哈希值。SHA-256 函数的图像呈现出一种高度均匀分布的特征,这意味着即使输入数据略微改变,输出的哈希值也会发生巨大变化,从而保证了哈希函数的抗碰撞性。
哈希函数在区块链中用于多种用途,包括生成区块的哈希、存储密码学货币的地址和交易签名等。
椭圆曲线加密是一种非对称加密技术,与 RSA 等其他加密算法相比,它提供了更高的安全性和更小的密钥尺寸。
在椭圆曲线加密中,参与者使用椭圆曲线上的点来生成公钥和私钥。发送方使用接收方的公钥对消息进行加密,而接收方使用自己的私钥对消息进行解密。
椭圆曲线加密的安全性基于一个称为“离散对数难题”的数学难题,即给定 \(P\) 和 \(Q = kP\),计算 \(k\) 的困难性。在适当选择的椭圆曲线上,这一问题是非常困难的。
在区块链中,三角函数图像扮演着关键的角色,尤其是在密码学和加密技术方面。密钥生成、哈希函数和椭圆曲线加密等领域都离不开这些函数的应用。通过理解这些概念,我们可以更好地理解区块链技术的基础,并设计更安全、更高效的系统。