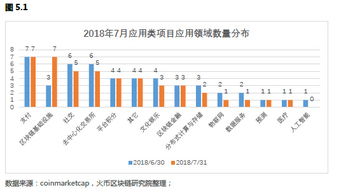
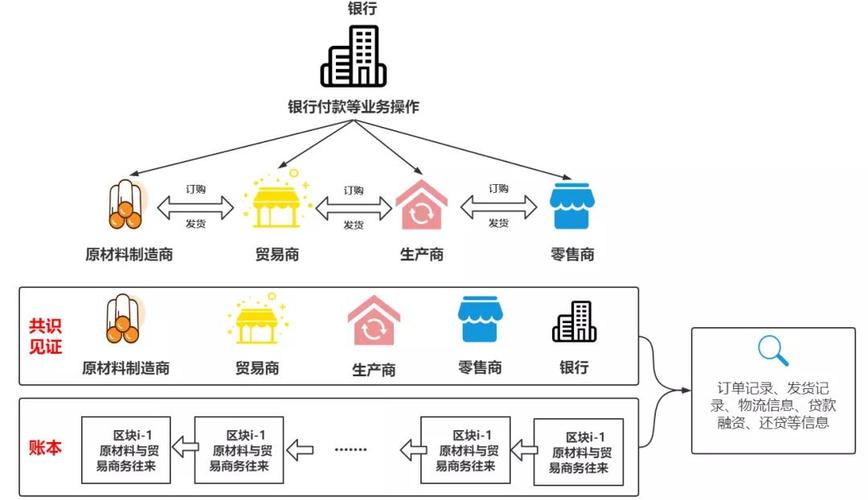
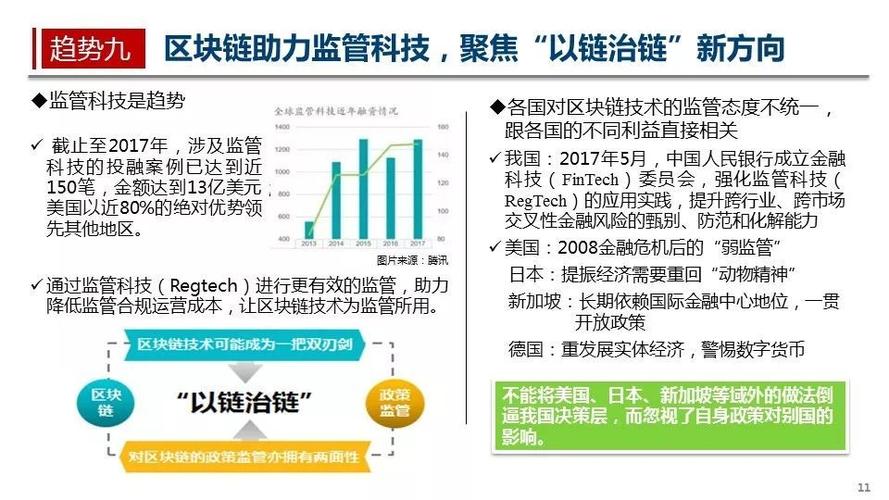
区块链应用领域及案例

区块链在数学中的应用案例

区块链技术是近年来备受瞩目的技术创新之一，它不仅在金融、供应链、社交媒体等行业中有广泛的应用，同时也在数学领域中产生了一些有趣而有价值的应用案例。本文将介绍几个区块链在数学中的应用案例，并探讨它们对数学领域的影响和潜在的未来发展。

一、安全加密与数字签名

区块链利用密码学的技术保障了数据的安全性。在数学中，散列函数和非对称加密算法是区块链中广泛应用的数学工具。散列函数保证了数据的不可逆性和唯一性，而非对称加密算法则实现了安全的数据传输和身份验证。

数字签名是区块链中的重要组成部分，它保证了交易的真实性和不可篡改性。通过使用非对称加密算法，数字签名能够确保交易的发起者不能否认其行为，并且其他人可以验证交易的真实性。在数学中，数字签名的实现依赖于椭圆曲线密码学和数论等数学理论。

二、去中心化的共识机制

区块链中的共识机制是保证数据一致性和可信度的基础，而去中心化是其核心特点之一。在数学中，共识机制可以通过博弈论和图论等数学模型进行建模和分析。

一种常见的共识机制是工作量证明（Proof of Work，PoW），其背后的数学思想是哈希算力的竞争。通过解决哈希问题来获得区块奖励，参与者需要消耗大量的计算资源，从而确保网络中的节点没有办法通过攻击来控制整个网络。另一种共识机制是权益证明（Proof of Stake，PoS），其核心原理是按照持有代币的多少来确定区块生成的权益。

三、分布式计算和智能合约

区块链技术的另一个重要特征是分布式计算和智能合约。智能合约是一种以代码形式存在的合约，其中包含了各种条件和规则，当满足条件时，合约会自动执行相应的操作。在数学中，智能合约可以通过形式化方法来进行验证和分析。

分布式计算是指利用区块链网络中的各个节点进行数据处理和运算，从而实现任务的协同完成。在数学中，分布式计算可以通过图论和优化理论等数学模型来分析和优化。

四、加密货币经济学

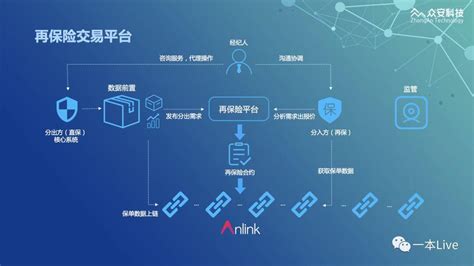
区块链技术的应用最为人熟知的是加密货币，如比特币和以太坊等。加密货币经济学是一个新兴的研究领域，涉及到货币的发行、价格、供需关系和市场机制等经济学问题。数学在加密货币经济学中发挥着重要的作用，例如通过价值函数和市场模型来解释加密货币的价格形成机制。

区块链在数学中有着广泛的应用，在安全加密、共识机制、智能合约、分布式计算和加密货币经济学等领域发挥了重要作用。数学为区块链提供了坚实的理论基础，同时也受到了区块链技术的推动和挑战。这些区块链在数学中的应用案例不仅推动了数学研究的发展，也为未来的科技创新和社会发展提供了新的思路和方法。